crmsetr.blogg.se - Atomic emission spectrum of hydrogen

#Atomic emission spectrum of hydrogen plus
#Atomic emission spectrum of hydrogen series

(1924), "The emission of nitrogen and hydrogen in infrared", J.

^ Paschen, Friedrich (1908), "Zur Kenntnis ultraroter Linienspektra.

(2009), "Accurate Atomic Transition Probabilities for Hydrogen, Helium, and Lithium", Journal of Physical and Chemical Reference Data, 38 (3): 565, Bibcode: 2009JPCRD.38.565W, doi: 10.1063/1.3077727 The energy differences between levels in the Bohr model, and hence the wavelengths of emitted or absorbed photons, is given by the Rydberg formula: 1 λ = Z 2 R ∞ ( 1 n ′ 2 − 1 n 2 ) : CS1 maint: untitled periodical ( link). Therefore the motion of the electron in the process of photon absorption or emission is always accompanied by motion of the nucleus, and, because the mass of the nucleus is always finite, the energy spectra of hydrogen-like atoms must depend on the nuclear mass.

#Atomic emission spectrum of hydrogen plus

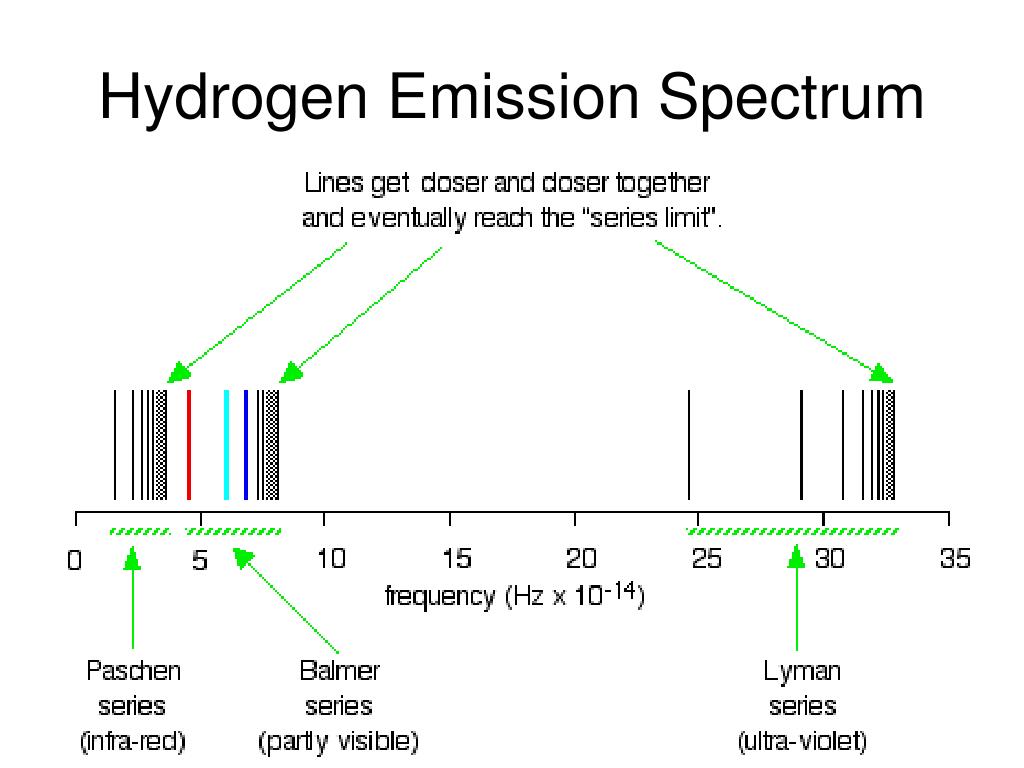
In the processes of absorption or emission of photons by an atom, the conservation laws hold for the whole isolated system, such as an atom plus a photon. In quantum mechanical theory, the discrete spectrum of atomic emission was based on the Schrödinger equation, which is mainly devoted to the study of energy spectra of hydrogenlike atoms, whereas the time-dependent equivalent Heisenberg equation is convenient when studying an atom driven by an external electromagnetic wave. The fine structure also results in single spectral lines appearing as two or more closely grouped thinner lines, due to relativistic corrections. These emission lines correspond to much rarer atomic events such as hyperfine transitions. There are emission lines from hydrogen that fall outside of these series, such as the 21 cm line. For example, the 2 → 1 line is called "Lyman-alpha" (Ly-α), while the 7 → 3 line is called "Paschen-delta" (Pa-δ).Įnergy level diagram of electrons in hydrogen atom Lines are named sequentially starting from the longest wavelength/lowest frequency of the series, using Greek letters within each series.

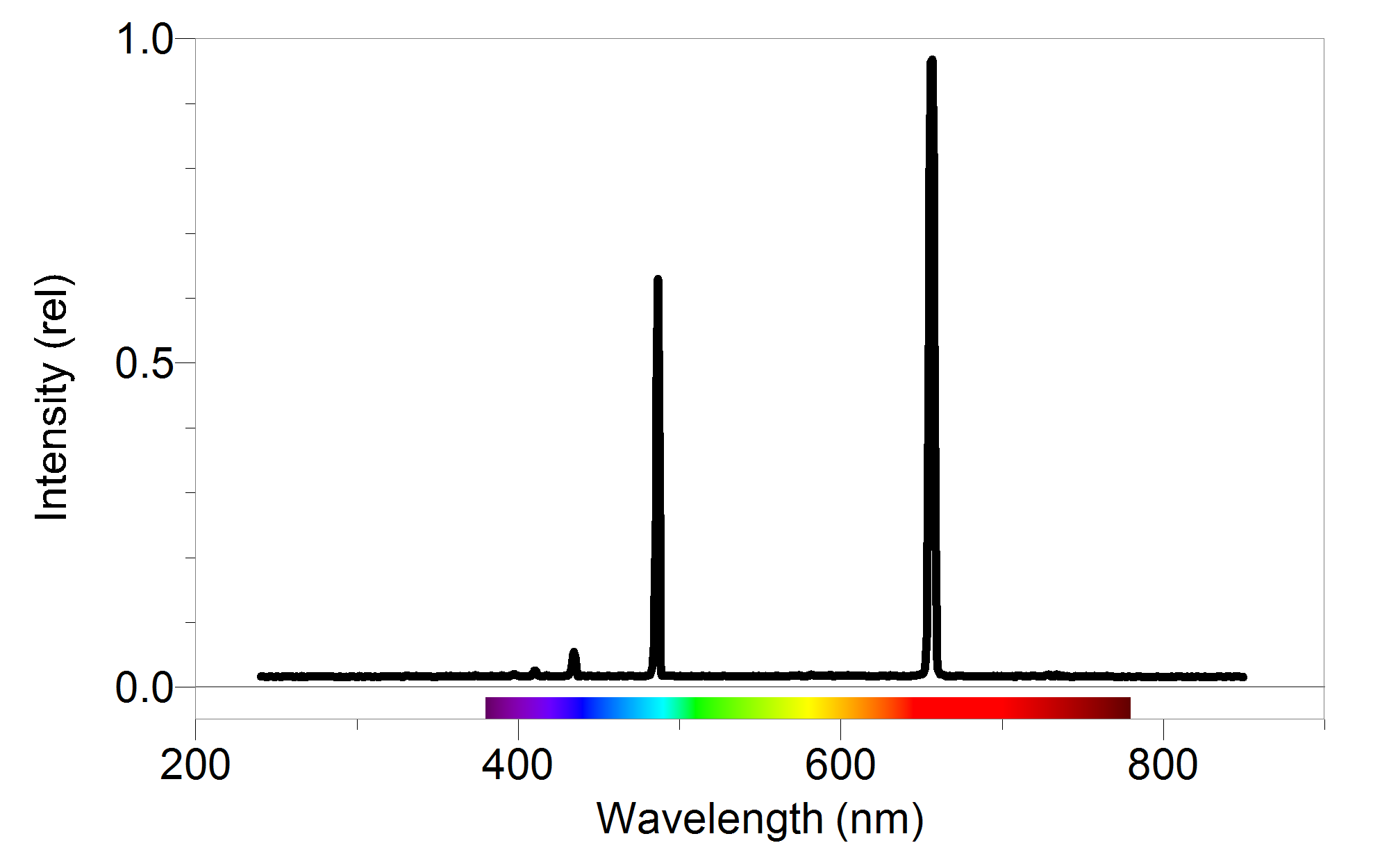
#Atomic emission spectrum of hydrogen series

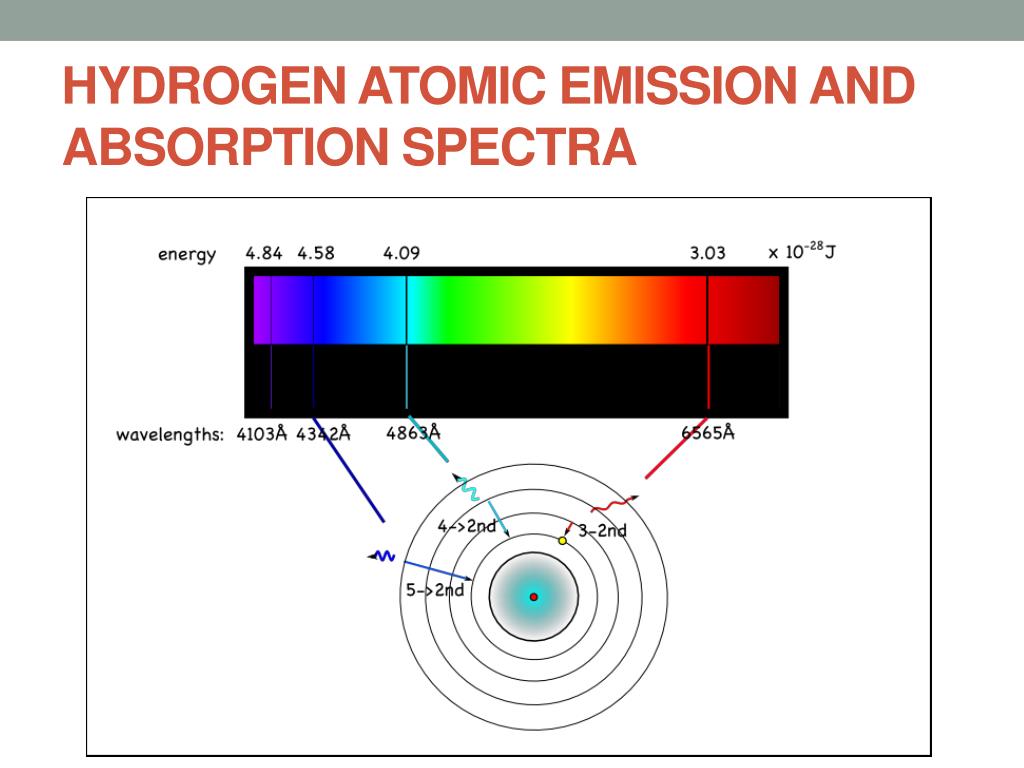
The spectral lines are grouped into series according to n′. Because the energy of each state is fixed, the energy difference between them is fixed, and the transition will always produce a photon with the same energy. The energy of an emitted photon corresponds to the energy difference between the two states. To distinguish the two states, the lower energy state is commonly designated as n′, and the higher energy state is designated as n.

Spectral emission occurs when an electron transitions, or jumps, from a higher energy state to a lower energy state. The Bohr model was later replaced by quantum mechanics in which the electron occupies an atomic orbital rather than an orbit, but the allowed energy levels of the hydrogen atom remained the same as in the earlier theory. Each energy level, or electron shell, or orbit, is designated by an integer, n as shown in the figure. These states were visualized by the Bohr model of the hydrogen atom as being distinct orbits around the nucleus. The electromagnetic force between the electron and the nuclear proton leads to a set of quantum states for the electron, each with its own energy. Energy levels are not to scale.Ī hydrogen atom consists of an electron orbiting its nucleus.

Further information: Hydrogen atom Electron transitions and their resulting wavelengths for hydrogen.